Parity Games: McNaughton-Zielonka Algorithm

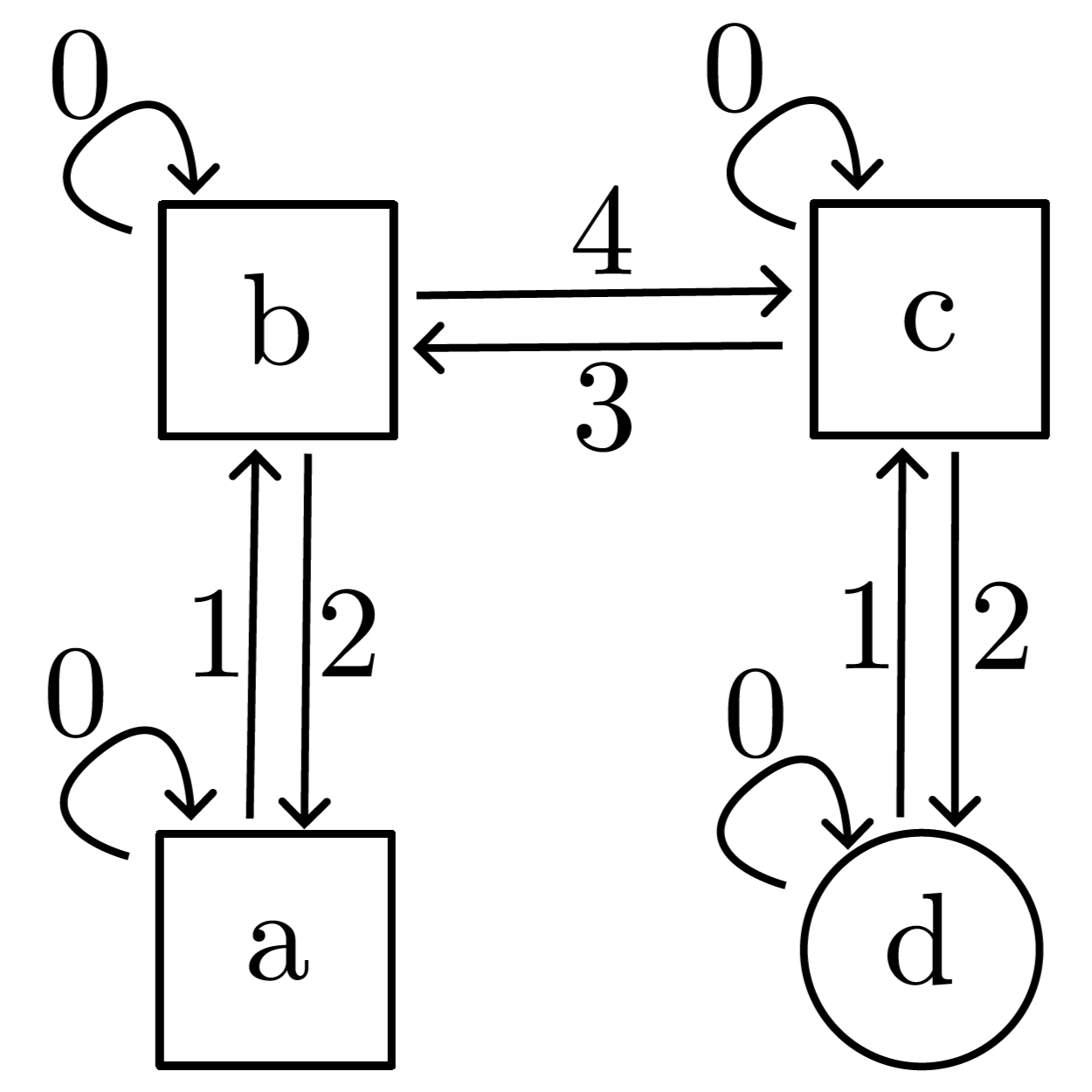
A very short Introduction to the Topic

Parity games are based on the concept of finite state devices. You might be reminded of NFA's (non-deterministic finite automata). They combine aspects of parity automata and reachability games and are used to model non-terminating interaction between a system and some environment. The states are partitioned to belong to two players - typicall called Adam and Eve - and whose transitions are controlled by their respective player. All nodes have a parity value (sometimes called priority or prio) assigned to them. Some other models use parity values as transition labels; these models are easily interchangable. A run (or play) is winning for Adam if the largest prio seen an unlimited amount of times during the run is odd, and winning for Eve if it is even. We are only considering deadlock-free games where these runs can happen (maximal plays). Note that these games are zero-sum games and for the winning regions note that $Q = W_E \uplus W_A$. A node is part of the winning region if there is a positional strategy $\sigma$ from that node where the player (typically Eve) has determined circle in $G\downharpoonleft_\sigma$ (the game where all transitions not in $\sigma$ are removed and only Adam controls the game) with the max prio being even (in this case). The proof of this claim by Zielonka is the base principle this algorithm is built upon. The question about how one might determine these winning regions still remains. This is what this algorithm is about. There are algorithms that run in quasi-polynomial time that use reductions with reachabilty games; this one does not. I might cover that in the future.

A parity game is a tuple $$ G = (Q_E, Q_A, E, \Omega) $$ where $Q_E$ are the nodes that belong to Eve and $Q_A$ are the nodes that belong to Adam. $E$ is the set of transitons and $\Omega: Q \rightarrow \mathbb{N}$ a function that maps nodes to prio values (we could also talk about game arenas with winning conditions here but the terms are not very strictly defined). Such a winning condition would be a set $$ C := \{\rho \in Q^\omega \mid \text{max inf } \rho \text{ even/odd}\} $$ The algorithm also uses a few other key concepts that were not mentioned yet: $$ Attr_X(K) := \{q \in Q_X \mid \exists q' \in X: (q, q') \in E\} \cup \{q \in Q_\overline{X} \mid \forall q' \in Q: (q, q') \in E \rightarrow q' \in K\} \cup K $$ is the reachability attractor of some set of nodes $K$ for player $X$. When talking about reach games, safety attractors are also relevant, but that is not our concern right now. Basically, this operation adds all of the nodes to a set that either belong to a player $X$ and have a transition into the set or that belong to the opponent $\overline{X}$ and only have transitions into the set. We can use this operation with the Kleene star and find a fix point that we call $Attr_X^*$. We can use this to make statements about the control structure of certain regions in the game. We can use that information to locate the winning regions recursively.

This is really short and lacks a lot of depth, but I figured that this might be enough for the time being and this page is dedicated towards the algorithm after all.

The Algorithm

The input to our function $zielonka$ is the Game $G$. We return the winning regions $W_E$ and $W_A$. First, find $$ k = \max\{\Omega(q) \mid q \in Q\} $$ If $k = 0$, then Eve wins everywhere. Otherwhise, determine the player of the function call: $$ X := \text{Eve if k is even else Adam} $$ We then search for all the nodes with prio $k$ and compute the attractor of that set of nodes. $$ K = \{q \in Q \mid \Omega(q) = k\} $$ $$ A_X = Attr_X^*(K) $$ We construct a subgame without the nodes in the attractor and make a recursive call. We then look at the attractor of the winning region of the opponent $\overline{X}$ in the entire game of the base call. $$ W_E', W_A' = zielonka(G\downharpoonleft_{Q \setminus A_X}) $$ $$ B = Attr_\overline{X}^*(W_\overline{X}') $$ We the make a second recursive call and determine the winning region of the player in the subgame without $B$. $$ W_E'', W_A'' = zielonka(G\downharpoonleft_{Q \setminus B}) $$ In the end we can return: $$ W_X = W_X'' $$ $$ W_\overline{X} = W_\overline{X}'' \cup B $$

We need both recursive calls to make shure that the strategies that the winning regions computed in the recursive calls are based on are actually valid in the full game. It might be the case that forming the subgames potentially removes transitions from the game. That can change the way the players are able to control the game. The attractor only cares about transitions and not about prio values. That means that there are nodes where you can not be shure about their belonging to a winning regions just by looking at the attractor control structure in the game. For example, the set $K$ is part of the attractor, but no one knows wether or not it is part of the winning region and if its attractor is entirely useful.

Output

The C++ implementation does exactly that and also outputs every step of the iteration in the algorithm in every recursive call.
This is what an example ouput looks like:

max prio is 4
K = {e, f}
Attr_E = {g, a, b, h, e, f}
created subgame with nodes: {c, d, i}
max prio is 3
K = {i}
Attr_A = {i}
created subgame with nodes: {d, c}
max prio is 1
K = {c}
Attr_A = {d, c}
created subgame with nodes: {}
max prio is 0
return base case prio 0: W_E = {}, W_A = {}
W_A' == Q\Attr_E -> return W_E = {}, W_A = {d, c}
W_A' == Q\Attr_E -> return W_E = {}, W_A = {c, d, i}
B = Attr_A(W_A') = {e, c, d, i}
subgame with Q\B: {a, b, f, g, h}
max prio is 4
K = {f}
Attr_E = {a, b, f}
created subgame with nodes: {h, g}
max prio is 2
K = {h}
Attr_E = {g, h}
created subgame with nodes: {}
max prio is 0
return base case prio 0: W_E = {}, W_A = {}
W_A' == Q\Attr_E -> return W_E = {h, g}, W_A = {}
W_A' == Q\Attr_E -> return W_E = {a, b, f, g, h}, W_A = {}
Eve: return W_E = {a, b, f, g, h}, W_A = W_A' u B = {i, d, c, e}
-----------------------------------------------------
EVE: {a, b, f, g, h}
ADAM: {i, d, c, e}

The corresponding parity game is hard-coded in the project and can be inspected in the repository.